Sorting Algorithms : Insertion Sort
插入排序的定义(Insertion Sort Definition)
Wikipedia 上对插入排序(Insertion Sort)描述:
是一种简单直观的排序算法,可以一次构建出项最终排序数组(或列表),是一种原地(in-place)的比较排序。
创建已排序的子列表,对于未排序元素,在已排序子列表中从右向左扫描,找到相应位置并插入
在从右向左扫描过程中,需要反复把已排序元素逐步向右挪位,为最新元素提供插入空间
以此类推,直到所有元素均排序完毕。
与大多数高级算法(如 快速排序(Quick Sort)、堆排序(Heap Sort) 或 归并排序(Merge Sort))相比,它在大量数据的列表上的效率要低得多。
比大多数其他简单的二次(即 O(n^2))算法(如 选择排序(Selection Sort) 或 冒泡排序(Bubble Sort))效率更高。
算法示例(Example)
以列表中的第一个元素作为已排序子列表,其余元素作为未排序子列表。
取第二个元素赋值给
key,然后比较key与第一个元素,如果第一个元素大于key,则将key插入到第一个元素前面。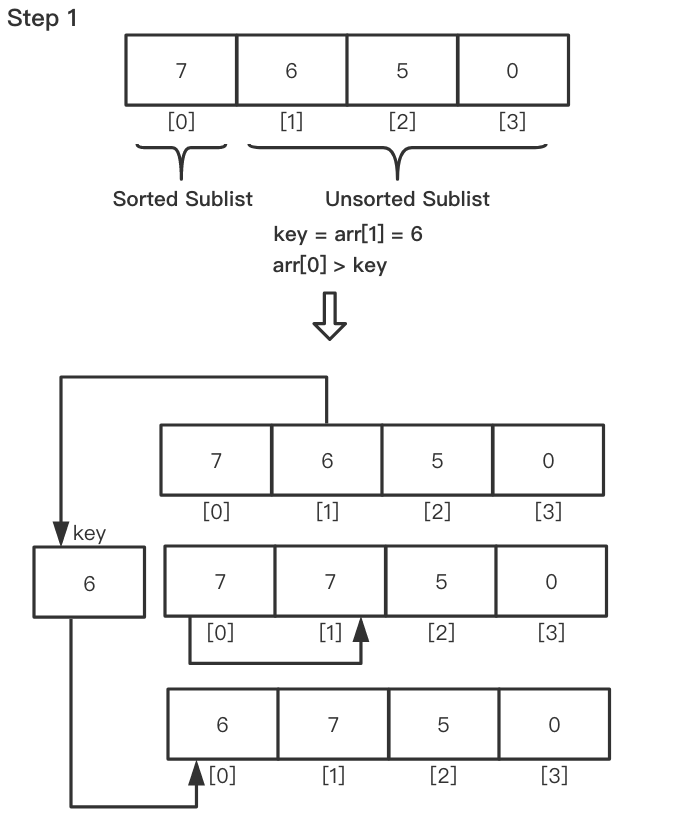
取第三个元素并将其与左侧的元素进行比较。将它放在比它小的元素后面。如果没有小于它的元素,则将其放在数组的开头。
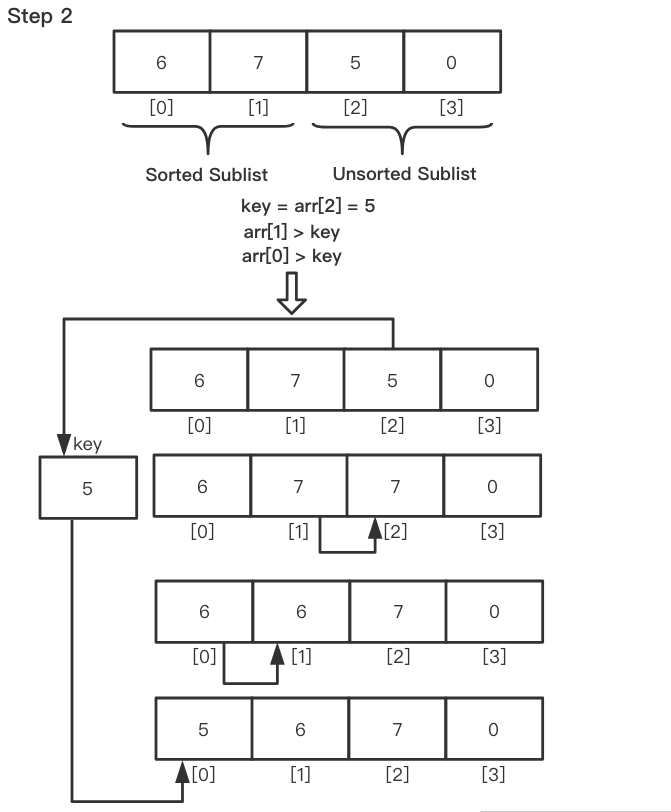
以此类推,将每个未排序的元素放在正确的位置。
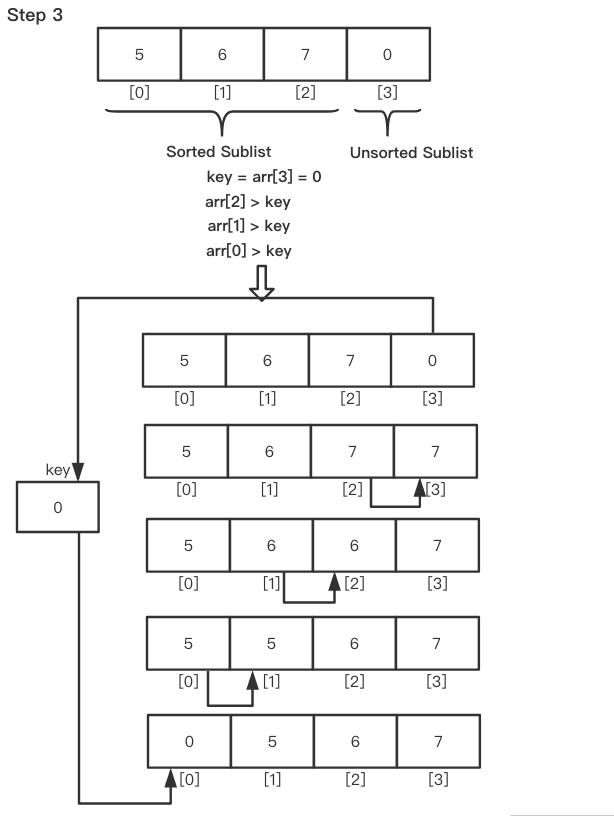
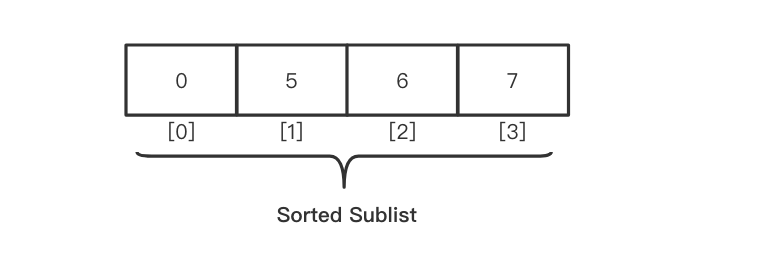
算法复杂度(Algorithm Complexity)
时间复杂度(Time Complexities):
最坏情况的复杂度:
O(n^2)假设,数组按升序排序,但目的是为了对列表进行降序排序。在这种情况下,那么最坏的情况就会发生。
必须将每个元素与其他元素进行比较,因此,对于每次第
n个元素,进行(n - 1)次比较,所以总的比较数 为n * (n - 1),约等于n^2最好情况的复杂度:
O(n)当列表已经是有序时,外循环运行
n次,而内循环根本不运行。所以,只有n个比较。因此,复杂度是线性的。平均情况的复杂度:
O(n^2)当数组的元素是混乱的顺序(既不是升序也不是降序)时,就会发生这种情况。
空间复杂度(Space Complexity):
- 因为需要一个临时变量 key ,因此空间复杂度为
O(1)
稳定性(Stability):
稳定性概念
如果 a 原本在 b 前面,而 a = b,排序之后 a 仍然在 b 的前面,那么说明该排序是稳定的,反之说明该排序是不稳定的。插入排序是稳定的(Stable)
插入排序的应用(Insertion Sort Applications)
插入排序使用于以下的情况:
需要排序的列表中的元素数量很少
需要排序的列表中,只有少数元素需要排序
代码实现(Code and Implementation)
C 语言实现
// C program for implementation of insertion sort
#include <stdio.h>
// n 为第几个元素
void insert(int arr[], int n) {
int key = arr[n];
int i = n;
while (i > 0 && arr[i - 1] > key) {
arr[i] = arr[i - 1];
i--;
}
arr[i] = key;
}
void insertionSort(int arr[], int n) {
int i;
// 认为第一个元素是在已排序子列表中,从第二个元素开始,将元素插入到已排序子列表中
for (i = 1; i < n; i++) {
insert(arr, i);
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n) {
int i;
for (i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
// Driver program to test insertion sort
int main() {
int arr[] = {7, 6, 5, 0};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Array before sorting: \n");
printArray(arr, n);
insertionSort(arr, n);
printf("\nArray after sorting: \n");
printArray(arr, n);
return 0;
}
