排序算法: 选择排序（Select Sort）

2019.07.28

Sorting Algorithms : Selection Sort

选择排序的定义（Selection Sort Definition）

Wikipedia 上对选择排序（Selection Sort）描述：

是一种简单直观的排序算法，是一种原地（in-place）的比较排序。

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
以此类推，直到所有元素均排序完毕。

它具有 O(n^2) 时间复杂度，所以在有着大量数据的序列中执行效率低下，并且通常比与它相似的插入排序（Insertion Sort）执行效率更低。

但选择排序以其简单性著称，在某些情况下，特别是在计算机存储器（Computer Data Storage）数量有限的情况下，它比其他更复杂的算法具有性能优势。

算法示例（Example）

从右到左循环遍历 n - 1 次列表，第一次循环遍历列表时，从列表中找出未排序子列表中的最大值（maximum）的下标值 pos，然后通过交换下标值为 pos 元素和下标值为 n -1 元素（即把最大值存放到列表中的已排序子列表中）,然后列表长度 n 进行减 1 操作。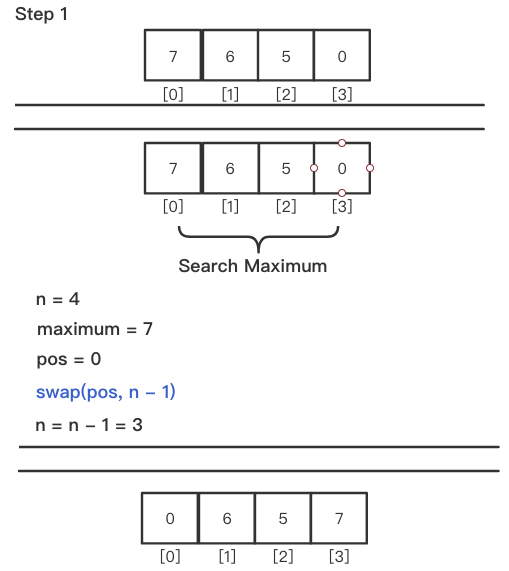
对于剩余的循环，将执行步骤 1 相同的过程。直至到循环遍历完第 n - 1 次时，列表排序完成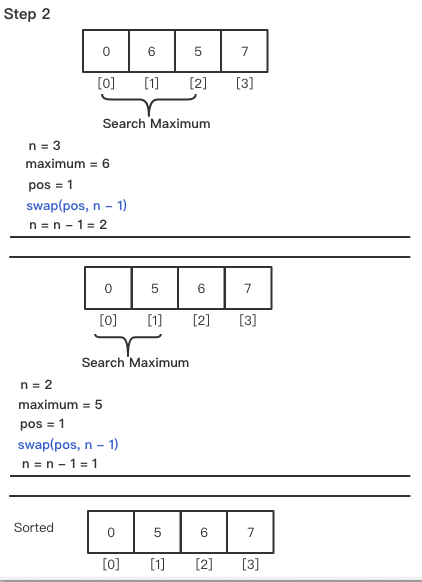

算法复杂度（Algorithm Complexity）

Pass	Number of Comparisons
`1st`	`(n - 1)`
`2nd`	`(n - 2)`
`3rd`	`(n - 3)`
`...`	`...`
`last`	`1`

总的比较次数：(n - 1) + (n - 2) +(n - 3) + ... + 1 = n(n - 1) / 2 接近等于 n^2，因此复杂度为 O(n^2)

同时我们可以通过简单地观察循环次数来分析复杂性，因为算法使用了 2 个循环，因此复杂度为 O(n * n ) =O(n^2)

时间复杂度（Time Complexities）：

最坏情况的复杂度：O(n^2)

如果我们想按升序排序数组，但数组已经是按照降序排列好的，那么最坏的情况就会发生。
最好情况的复杂度：O(n^2)

如果数组已经是排序完成。
平均情况的复杂度：O(n^2)

当数组的元素是混乱的顺序（既不是升序也不是降序）时，就会发生这种情况。

选择排序的时间复杂度在所有情况下都是相同的。在每一步，都必须找到最小元素（最大元素）并将其放在正确的位置。在未到循环结束之前，都不能确定最小元素（最大元素）。

空间复杂度（Space Complexity）：

因为需要一个临时变量 temp 用于交换，因此空间复杂度为 O(1)

稳定性（Stability）：

稳定性概念

如果 a 原本在 b 前面，而 a = b，排序之后 a 仍然在 b 的前面，那么说明该排序是稳定的，反之说明该排序是不稳定的。

选择排序是不稳定的（Unstable）

选择排序的应用（Selection Sort Applications）

选择排序使用于以下的情况：

小量数据的列表。
不需考虑交换元素的成本
强制性需要检查所有的元素
写入存储器的成本与闪存相同（与冒泡排序的 O(n2) 相比，选择排序的写入/交换次数为 O(n)）

代码实现（Code and Implementation）

C 语言实现

// C program for implementation of selection sort 

#include <stdio.h>
void swap(int arr[], int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// Find the maximum element position in unsorted array
int findMaximumPos(int arr[], int n) {
    int max = arr[0];
    int pos = 0;
    int i;
    for (i = 1; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
            pos = i;
        }
    }
    return pos;
}

void selectionSort(int arr[], int n) {
    // 从右到左循环遍历 n - 1 次数组
    while (n > 1) {
        int pos = findMaximumPos(arr, n);
        swap(arr, pos, n - 1);
        n--;
    }
}

// Function to print an array
void printArray(int arr[], int size) {
    int i;
    for (i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

// Driver program to test above functions
int main() {
    int arr[] = {7, 6, 5, 0};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("Array before sorting: \n");
    printArray(arr, n);
    selectionSort(arr, n);
    printf("\nArray after sorting: \n");
    printArray(arr, n);
    return 0;
}

参考（References）

排序算法 Sorting Algorithm

△

Vivi's Blog