Sorting Algorithms : Shell Sort
希尔排序的定义(Shell Sort Definition)
Wikipedia 上对希尔排序(Shell Sort)描述:
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本,是一种原地(in-place)的比较排序。
首先对存在间隔的元素进行排序,然后逐渐减小要比较的元素之间的间隙
从间隔大的元素开始,这样会比其他简单的比较排序更快地将未排序的元素移动到正确的位置。
希尔排序的核心在于间隔序列。
间隔序列(Gap Sequences)的取法:
最初 Donald Shell 提出取间隔(增量)序列(Gap Sequences)为 {n / 2, (n / 2) / 2, ..., 1 }
Knuth 提出取间隔(增量)序列递推式(Gap Sequences)为 h(1) = 1, .., h(i) = 3 * h(i - 1) + 1
Hibbard 间隔(增量)序列递推式:h(1) = 1, h(i) = 2 * h(i - 1) + 1
算法示例(Example)
排序列表共有
n个元素,取整数gap(gap < n)作为间隔,将列表分成gap个子列表,所有距离为gap的元素放在同一个子列表中。对每个子列表分别进行插入排序
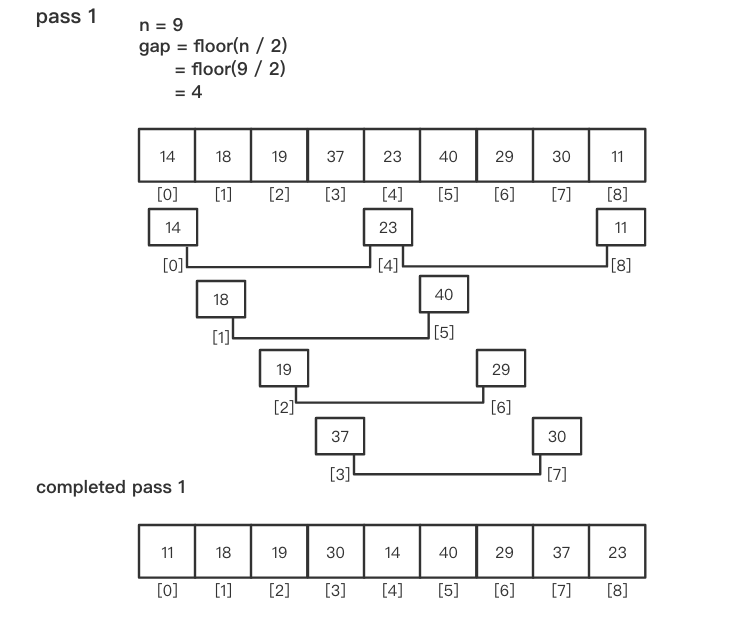
然后缩小间隔
gap,如取gap = gap / 2,重复步骤 1,划分和排序子列表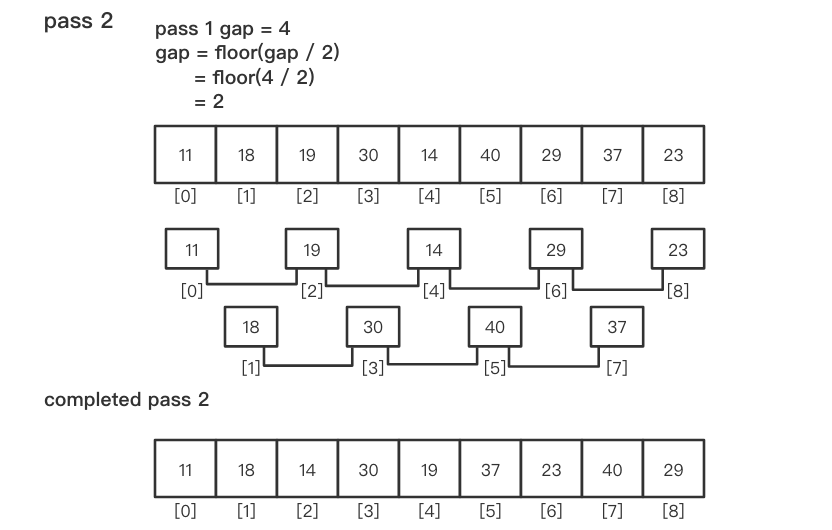
直至
gap = 1时,对整个列表进行插入排序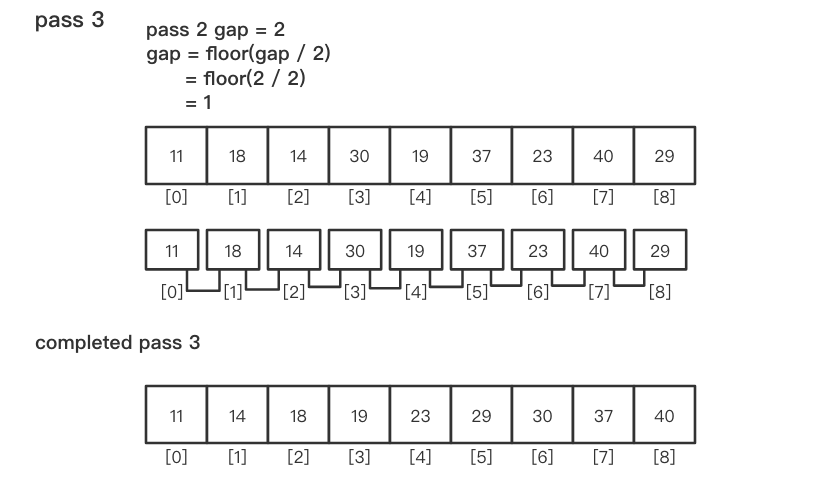
算法复杂度(Algorithm Complexity)
时间复杂度(Time Complexities):
最坏情况的复杂度:小于或等于
$\displaystyle O(n^{2})$希尔排序的最坏情况时间复杂度总是小于或等于
$\displaystyle O(n^{2})$希尔排序的最坏情况时间复杂度与取间隔序列策略有关
最好情况的复杂度:
$\displaystyle O\left(n\log^{2}n\right)$当数组已经排序时,每个间隔(或增量)的总比较数等于数组的大小。
平均情况的复杂度:
$\displaystyle O\left(n\log^{2}n\right)$希尔排序的平均情况的复杂度与取间隔序列策略有关,在
$\displaystyle O(n^{1.25})$附近。
时间复杂度取决于所选的间隔序列。对于所选择的不同增量序列,上述复杂度不同。最佳增量序列未知。
空间复杂度(Space Complexity):
- 因为需要一个临时变量 key ,因此空间复杂度为
O(1)
稳定性(Stability):
稳定性概念
如果 a 原本在 b 前面,而 a = b,排序之后 a 仍然在 b 的前面,那么说明该排序是稳定的,反之说明该排序是不稳定的。希尔排序是不稳定的(Unstable),因为希尔排序算法不检查位于间隔之间的元素。
希尔排序的应用(Shell Sort Applications)
希尔排序使用于以下的情况:
对于调用堆栈是一种开销的行为
递归超出限制
当值靠近的元素在间隔很远时,插入排序不能很好地执行。 希尔排序是有利于减少关闭元素之间的距离,因此会减少执行的交换次数。
代码实现(Code and Implementation)
C 语言实现
// C program for implementation of shell sort
#include <stdio.h>
// n 为第几个元素,gap 为当前间隔增量
void insert(int arr[], int n, int gap) {
int key = arr[n];
int i = n;
// 如果该组元素中,前几个元素都比 a[i] 大,则执行后移,把比 a[i] 大的都移动到 a[i] 后面
while (i > 0 && arr[i - gap] > key) {
arr[i] = arr[i - gap];
i = i - gap;
// 当 i - gap 后比 gap 小,说明已经排好序,这时退出循环
if (i < gap) {
break;
}
}
arr[i] = key;
}
// n 为列表中元素个数,gap 为当前间隔增量
void insertionSort(int arr[], int n, int gap) {
int i;
// 进行插入排序,从每个分组的第 gap 个元素开始,而不是从它的第 1 个元素开始
for (i = gap; i < n; i++) {
insert(arr, i, gap);
}
}
void shellSort(int arr[], int n) {
int gap = 1;
// Knuth增量序列递推式:h(1) = 1, h(i) = 3 * h(i-1) + 1
while (gap < n) {
gap = gap * 3 + 1;
}
// 间隔增量 gap 每次变小,直到为 1
while (gap > 0) {
// 进行插入排序,从每个分组的第 gap 个元素开始,而不是从它的第 1 个元素开始
insertionSort(arr, n, gap);
gap = (gap - 1) / 3;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n) {
int i;
for (i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
int arr[] = {14, 18, 19, 37, 23, 40, 29, 30, 11};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Array before sorting: \n");
printArray(arr, n);
shellSort(arr, n);
printf("\nArray after sorting: \n");
printArray(arr, n);
return 0;
}
